This is based on my dissatisfaction with the messed up way time and work problems are handled in quantitative aptitude examination guides. They take a simple idea, threaten you with time constraints and leave you feeling broken and guilty because you couldn't solve them quickly enough.

And having an education in fundamental electrical engineering, I couldn't help but notice the underlying symmetry between

\[ \text{Amount of work} = \text{Speed of work} \times \text{Time taken} \]

and

Ohm's Law, given by \[ V = IR \]

So, this is my proposal. Model the given time and work problem as a very simple resistive network and the problem will solve itself!

Analogies obtained from the formula

Amount of work is analogous to Voltage Speed of work is analogous to Current Time taken is analogous to Resistance

A few simple problems I have worked out using this analogy are shown below. Much more are available in the pdf available for download at the end of this page.

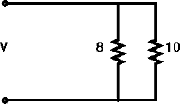
Worker A takes 8 hours to do a job. Worker B takes 10 hours to do the same job. How long should it take both A and B working together, but independently, to do the same job?

\[ R_a = 8 \] \[ R_b = 10 \] A and B working together is analogous to Ra || Rb \[ R_a || R_b = \frac{40}{9} \; \text{days} \] The parallel resistance makes sense when you think of workers A and B working in parallel. So, their individual speeds of working (currents) add up.

The Ohm's Law analogy also holds good for the pipes-cisterns class of problems, with leaks being modelled as negative resistances. I have shown the working of a simple example below.

An electric pump can fill a tank in 3 hours. Because of a leak in the tank, it took 3½ hours to fill the tank. If the tank is full, how much time will the leak take to empty it?

\[ R_a = 3 \] \[ R_a || R_b = \frac{7}{2} \] Solving, \[ R_b = -21 \] Therefore, the leak will take 21 hours to empty the tank.