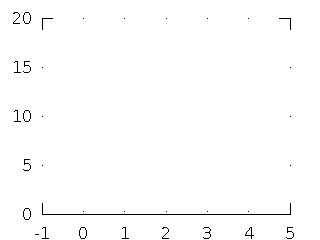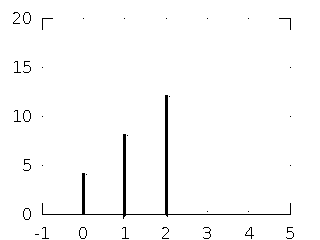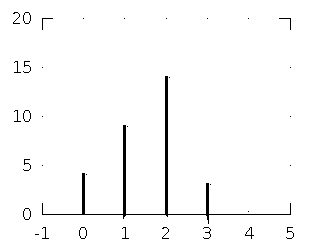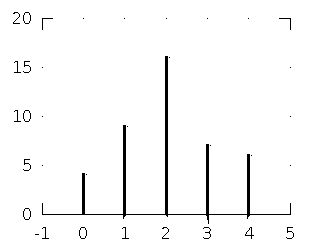The process of convolution works on the twin concepts of linearity and shift invariance.

To calculate the output of a system with impulse response \( h[n] = \{1,2,3\} \) when the input is \( x[n] = \{4,1,2\} \), we convolve x[n] and h[n] to get the output.

Mathematically,

\[ y[n] = x[n] \ast h[n] \]

Instead of considering the input signal as a whole, we break it up into a combination of impulses.

Therefore

\[ x[n] = 4\delta[n]+\delta[n-1]+2\delta[n-2] \]

So, we calculate the response for each sample (which is proportional to the impulse response), and add up all the responses.

Partial output for \( 4\delta[n] \) is \[ 4h[n] = \{4, 8, 12\} \] Partial output for \( \delta[n-1] \) is \[ h[n-1] = \{0, 1, 2, 3\} \] Partial output for \( 2\delta[n-2] \) is \[ 2h[n-2] = \{0, 0, 2, 4, 6\} \]

Summing up all the partial outputs, we get the total output,

\[ y[n] = 4h[n]+h[n-1]+2h[n-2] = \{4,9,16,7,6\} \]