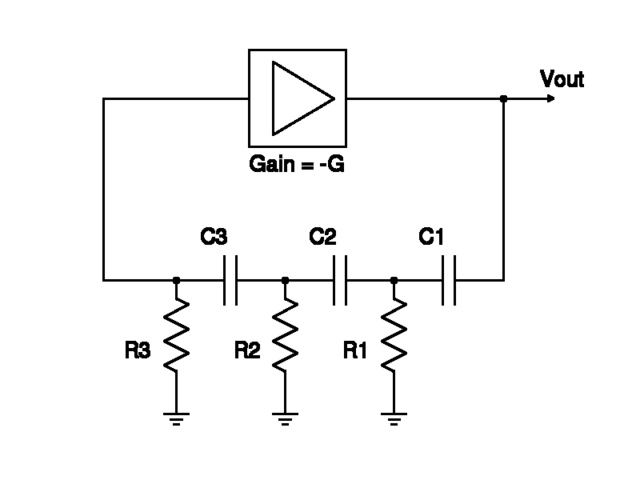
RC Phase Shift Oscillator - Oscillation Criteria
Published by Arun Isaac on
Tags: electronics, maxima
The principle of operation of the RC phase shift oscillator is reasonably simple. At the oscillation frequency, the three RC stages put together produce a phase shift of 180 degrees, the amplifier contributes the remaining 180 degrees phase shift, and thus positive feedback is established and the signal reinforces itself.
However, the math behind the oscillation criteria is surprisingly tedious due to the successive RC stages loading the previous ones. And, for non-identical RC stages (R1,R2,R3 are not equal and C1,C2,C3 are not equal), the math becomes way more tedious.
Three years back, when I first learnt about the phase shift oscillator, I worked out the oscillation criteria manually with pen and paper. Treating each RC stage as a two port network, I worked out the ABCD matrix of a single stage. Then, I simply cubed the ABCD matrix to get the ABCD parameters of the overall three stage RC network. The algebra was tedious but there is indeed some pleasure in such hack and slash algebra. The mental equivalent of a good gym workout, it is. The parameter ’A’ of the overall ABCD matrix gives the reciprocal of the transfer function of the RC feedback network. From there, applying the oscillation criteria (GH=1), the oscillation frequency and critical gain were easily obtained.
\[ f = \frac{1}{2 \pi \sqrt{6} R C} \]
For three identical RC stages, the math was though a bit tedious, workable. Three non-identical RC stages is however another story. Dealing with so many variables (R1, R2, R3, C1, C2, C3) instead of just two variables (R and C), I am not sure is humanly possible. Such tedium was certainly not within my pain threshold. So, the idea had to be put to rest. And so it has hibernated since. Until I found Maxima!
Maxima is a computer algebra system. That’s kinda like a calculator that can do algebra instead of just numerical calculations! I am aware that Matlab and GNU Octave do have symbolic libraries which do similar stuff, but I never really liked them. Octave’s symbolic libraries aren’t very complete either. I always felt that the treatment of “symbolic variables” in Matlab and Octave was more of a patch than anything. Maxima was however, just perfect! A sweet and elegant way to do algebra on a computer, I think!
So, I let Maxima cut through all the algebra of the RC phase shift network. Lo and behold, here we have the results, achieved almost painlessly!
\[ f = \frac{1}{2 \pi \sqrt{R_2R_3C_2C_3 + R_1R_3C_2C_3 + R_1R_3C_1C_3 + R_1R_2C_2C_3 + R_1R_2C_1C_3 + R_1R_2C_1C_2}} \]
For the benefit of the reader, I have also attached the Maxima batch files which did all the awesome work.